Integral adalah kebalikan dari proses diferensiasi. Integral ditemukan menyusul ditemukannya masalah dalam diferensiasi di mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. Lambang integral adalah 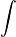
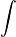
Integral terbagi dua yaitu integral tak tentu dan integral tertentu. Bedanya adalah integral tertentu memiliki batas atas dan batas bawah. Integral tertentu biasanya dipakai untuk mencari volume benda putar dan luas.
Rumus umum dan bentuk - bentuk fungsi integral :

![\int [f(x) + g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx](http://upload.wikimedia.org/wikipedia/id/math/e/7/d/e7d070d203baf49797b4e4a3fc3685f3.png)
![\int f(x)g(x)\,dx = f(x)\int g(x)\,dx - \int \left[f'(x) \left(\int g(x)\,dx\right)\right]\,dx](http://upload.wikimedia.org/wikipedia/id/math/3/b/8/3b8eab67c2a13a6392f41a8854cb2348.png)
![\int [f(x)]^n f'(x)\,dx = {[f(x)]^{n+1} \over n+1} + C \qquad\mbox{(untuk } n\neq -1\mbox{)}\,\!](http://upload.wikimedia.org/wikipedia/id/math/0/7/2/072d6a84d5c3d598b8f7a8aa86cb2f44.png)

![\int {f'(x) f(x)}\,dx= {1 \over 2} [ f(x) ]^2 + C](http://upload.wikimedia.org/wikipedia/id/math/0/c/6/0c64f04cc80db157abf9bbb321648b42.png)
lumayan bagus blog anda..............
BalasHapusterimakasih...:D
Hapusterimakasih ardy :)
Hapusterimakasih aniez :)
Blog anda menolong makalah saya... terimakasih...
BalasHapusgak ngerti gan
BalasHapusThanks a lot
BalasHapusgvd
BalasHapusiwak pitik enak
BalasHapusiwak pitik enak
BalasHapus